Most children learn that written numbers represent quantities in pre-school or junior primary school.
Now our new study shows that honeybees too can learn to match symbols and numerosities, much like we humans do with Arabic and Roman numerals.

Human language and mathematics
Language is the ability to learn and use a system of symbolic representations for communication. This includes a capacity to relate signs to abstract information.
For example, letters grouped together make a word which we can read, and sounded words put together in the correct order allow us to have a conversation. Human language can incorporate spoken, written, visually signed, or tactile forms like braile.
Around the world humans have developed many different spoken and written languages. However, mathematics in particular is often regarded as a "universal language" since the mathematical concepts that describe values and equations do not depend on cultural or other frameworks.
We are interested in the question of whether numerical symbols are truly universal – that is, whether they also work for species that are not human.
The language of honeybees
The honeybee is a super organism for the study of comparative information processing in a brain. In 1973 Karl von Frisch was awarded a Nobel Prize in the field of Physiology and Medicine for his demonstrations that the honeybee can communicate with hive mates via a symbolic dance language.
von Frisch showed that a foraging bee which locates rewarding flowers can fly back to a hive and signal both the direction and distance of the nutritious flowers via a "waggle dance". Other bees can interpret the dance language to know where to fly to collect nectar.
We wondered if such an impressive communication system meant that honeybees could learn another type of symbolic language, a basic symbolic number system.
Interestingly, chimpanzees, Rhesus monkeys, pigeons, and a single African grey parrot named Alex have demonstrated the skill to learn either Arabic numerals or English names for numbers. This shows us that while no non-human species appear to have developed a symbolic representation of number, it is not because they lack the brain capacity to understand such representations.
Our work has already shown honeybees can learn and apply challenging numerical concepts such as greater vs. lesser items, a quantitative valuation of "zero", and simple arithmetic.
We took this knowledge a step further with our latest research.
How do bees learn?
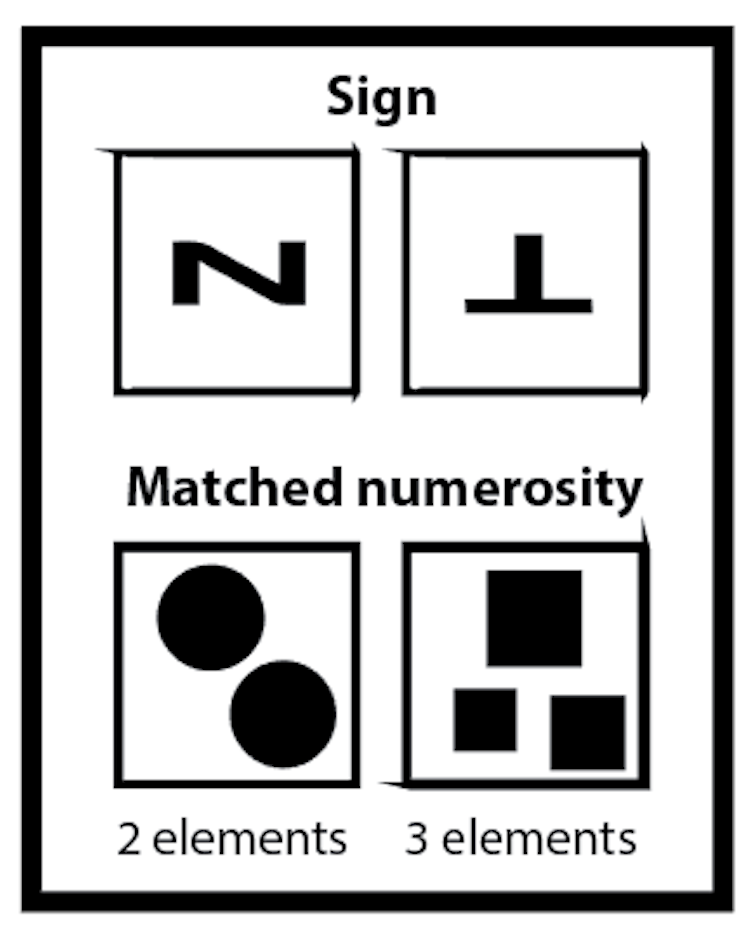
To train honeybees to match symbols (called "signs") and number amounts (called "numerosities"), we used a subset of the symbols previously used to train pigeons on a similar task.
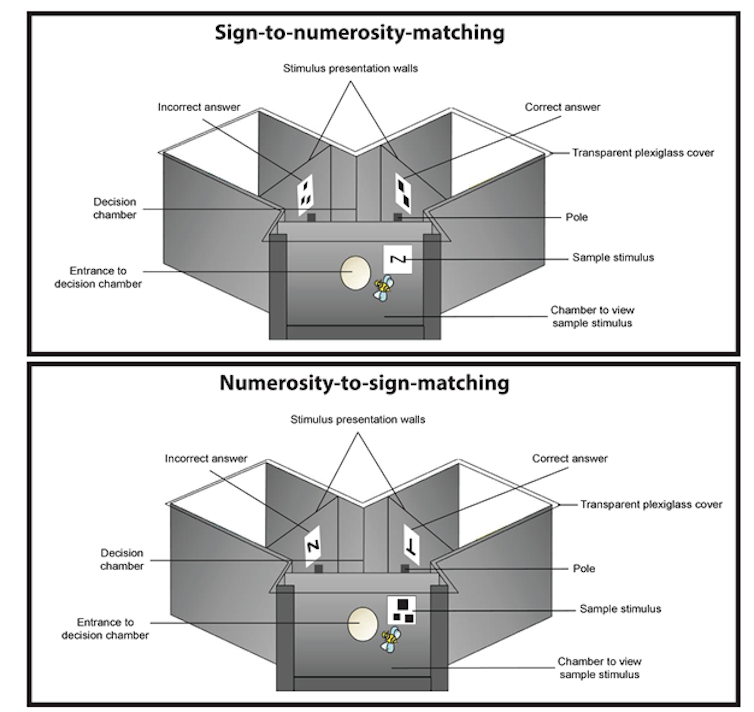
Bees were trained to fly into a Y-shaped maze. Inside the maze the bee would view a stimulus. The bee would then fly into the decision chamber were it would view two options, one correct and one incorrect.
One group of bees was trained to match a sign to a numerosity, while a second group was trained to match a numerosity to a sign.
If bees were learning to match a sign to a numerosity, they would first see the sign and then have the option to choose two or three shapes. If bees were learning to match a numerosity to a sign, they would first see a number of items, such as three squares, and then have the option to choose from two signs.
For example, if a bee viewed an N-shaped sign, she would need to choose a display presenting two items. She would need to be able to do this regardless of the shape, pattern, or color of the items presented.
If the bee chose correctly she would receive a sugar solution, but if she chose incorrectly, she would taste bitter quinine (which does not hurt the bee but is not pleasant for her). Importantly, neither the quinine nor the sugar can be smelled by the bee, so the only cue for decision making is the visual one.
Matching symbol to number
Bees were trained for 50 trials to match an N-shape sign with the number "two", and an inverted T-shape sign with the number "three", and achieved an accuracy of about 75 percent. This is the first time symbol matching to number has been shown in an invertebrate.
After training was completed bees were tested in several conditions with completely novel patterns, colors and shapes and continued to prefer to match the sign with the numerosity, or the numerosity with the sign.
Interestingly, however, we found bees were unable to reverse their learnt tasks. If a bee had learnt to match a sign to a numerosity, she could not then match a numerosity to a sign, or vice versa. It appears the association between the number and the symbolic representation was only learnt in one direction and was unable to be reversed.
Interestingly, these kinds of learning outcomes – referred to as "operational schemas" – are sometimes applicable to how humans learn too.
What does this mean?
While no other species besides humans has spontaneously developed a language for numbers, our research suggests an insect can understand and learn basic representation of numbers through symbols.
The system we taught to bees was limited in several ways. For example, we trained bees to link just two quantities and two symbols. Also we do not yet know if bees gave quantitative value to the symbols; we simply know that they can link the symbol and quantity together.
And yet it is remarkable bees displayed some capacity to understand numbers through symbols.
We're left wondering whether we as humans are so very special after all – that perhaps the ability to learn mathematics could be universal.
Despite the limitations of the current research, we have demonstrated, to a small extent, symbolic communication with an insect species, which we have been separated from by over 600 million years of evolution.
Our research is laying the foundations for developing a communication system with very different animal species, and shows the differences between human and non-human animals are not as great in some regards as we might previously have thought.![]()
This article is republished from The Conversation by Scarlett Howard, Postdoctoral research fellow, Université de Toulouse III – Paul Sabatier; Adrian Dyer, Associate Professor, RMIT University, and Andrew Greentree, Professor of Quantum Physics and Australian Research Council Future Fellow, RMIT University under a Creative Commons license. Read the original article.
Không có nhận xét nào:
Đăng nhận xét